物理 第三部:流体の物理
☆ “ホーム” ⇒ “生活の中の科学“ ⇒ “基礎物理” ⇒
ここでは,流体中の物質に働く力に関し, 【完全流体中の物質に作用する力】, 【粘性流体中の物質に作用する力】, 【空気抵抗(抗力)とは】, 【レイノルズ数とは】, 【流体の抗力とは】, 【ストークスの式について】 に項目を分けて紹介する。
【完全流体中の物質に作用する力】
静止した流体中を物体が一定速度 v で移動している時,座標を物体に固定すると,流体が静止した物体に向かって一定速度 - v で流れていると解釈できる。
粘性を無視した取扱いができる完全流体(perfect fluid)の定常流体の中に,流れに対して対称な物体がある場合は,物体を避けるように流れが迂回する。このとき,物体回りの流線は物体の前後で対称形になる。
完全流体では,粘性による接線方向の力を受けないので,物体に作用する力は,物体の面に対して鉛直方向の力(垂直応力)のみである。
クッタ‐ジュコフスキーの定理(Kutta-Joukowski's theorem)
飛行機の翼などに発生する揚力(lift)を計算するために用いられる空気力学(aerodynamics)の基本理論である。
一様な流れ(一様流)の粘性のない流体中に,断面形の任意な柱状物体を,流れの方向に対し直角に置いた時,物体に対し流れの直角方向に作用する力,すなわち物体の軸方向の単位長さ当りの揚力 L は,
L= ρU Γ
で与えられる。なお,ρは流体の密度,U は一様な流れの速度,Γは物体の周りの循環(circulation)である。
循環とは,一様流に対して物体を置くと,物体を回る流れが誘発されるが,流体力学では,この流れの大きさ(渦の強さ)を示す量を循環(Γ:ガンマ)とよび,閉曲線上での流体の速度の線積分で与えられる。
定性的に示すと,翼を傾けて置いた時,翼の循環 Γは流速 U に比例し,傾きの大きさが大きいほど大きくなる。
従って,揚力は流体の密度ρ,流速 U の2乗に比例するとともに,翼の傾きの影響も受ける。
なお,揚力のモデル式は,動圧 1/2 ρU2,循環とストークスの定理で結び付けられる代表面積 S と揚力係数 CL を用いて,
L= 1/2 ρU2 S CL
で表されるのが一般的である。ここで, U は物体と流体の相対速度である。
ダランベールのパラドックス(D'Alembert's paradox)
静止している完全流体(粘性がない流体)中で,物体を等速直線運動させたとき,又は一様流の中に物体を置いた時,物体に抗力(drag)が働かないという定理(逆理)である。
この定理には,何ら矛盾はないが,実在の流体での経験(抗力が計測される)に反するため,俗にパラドックスと称されるようになった。
ここで,完全流体の一様流の中に円柱を置いた場合を考える。一様流の速度の大きさを U ,密度ρ,円柱から無限遠の圧力を P∞ とした時,円柱回りの圧力分布 p(θ) は,ベルヌーイの式から,
![]()
と書ける。ここで,p0 は,θ= 0 , πで流速 0 となる点(よどみ点)の圧力である。
従って,円柱表面上の圧力は,
![]()
となる。
円柱にかかる圧力の合力 を P( Px,Py ),n を円柱表面の単位法線ベクトルとし,上式を用いて全周にわたって積分

すると,結論として,Px = 0 ,Py = 0 となる。
すなわち,圧力分布が上下 (前後)対称で,力の向きは上下(前後)の部分でそれぞれ反対方向に向い,円柱には流れの抗力が働かないことになる。
このパラドックスが生じる原因は,無限遠方まで広がる 1 種類の流体で,粘性を考慮しないこと,重力などの体積力を考慮しないこと,連続の一様流であること,物体が単独で存在することを前提としているためである。従って,前提のいずれかが成り立たない場合は抗力が発生する。
【参考:基礎用語】
- 揚力(lift)
飛行機の翼に対して働く力のうち,進行方向に直角な成分をいう。これを一般化し,流れの中にある物体,又は流体中を進行する物体に働く力(合力)のうち,流れや進行方向と直角の方向に作用する力をも揚力という。
揚力は,物体の相似比の二乗と流体の密度と流速の二乗の積に比例する。 係数が異なるだけで抗力と同形式である。 - 揚力係数(lift coefficient)
物体の形状,迎角,流体の物性,マッハ数,レイノルズ数などにより変わる。迎角が小さいときの揚力係数はほぼ迎角に比例し,迎角が大きいと流れの剥離で揚力係数が急激に小さくなる。空気中の揚力係数は地面や水面の近くで大きくなる(地面効果)。 - 動圧(dynamic pressure)
ベルヌーイの定理における流体の運動エネルギーを表わす項 1/2 ρv2 をいう。 - ストークスの定理(Stokes' theorem)
ガウスの定理,平面のグリーンの定理などと並んで,ベクトル解析分野で最も重要な積分定理の一つである。
ストークスの定理は,三次元の閉曲面を境界とする曲面上で定義された関数の線積分と面積分を関係づける定理で,イギリスの物理学者ストークスに因み命名された。 - ストークス(Sir George Gabriel Stokes)
サー・ジョージ・ガブリエル・ストークス(1819年~1903年)は,アイルランドの数学者,物理学者で,ストークスの式,粘度など単位,ストークス散乱などで知られる。 - 抗力(drag)
流体中を運動する物体,又は流体中に置かれた物体に,物体の運動と逆向き,流体の流速と同じ向きに働く力をいい,航空機や船舶などの流体力学分野で用いられる用語である。
なお,抗力(drag)を構成する摩擦抵抗(粘性抵抗)は概ね速度に比例し,圧力抵抗(慣性抵抗)は概ね速度の 2 乗に比例する。一方,抗力(reaction)の動摩擦力は,速度に依存しない力であり,日本語の用語は似ているが,特性に大きな差がある。
単に,抗力といった場合は,流体中の物体に働く抗力(drag)を指す場合が多い。
ページの先頭へ
【粘性流体中の物質に作用する力】
実用の流体は,多少なりとも粘性を有する。ナビエ–ストークス方程式は,粘性流体の運動を記述する 2 階非線型偏微分方程式で,NS 方程式とも略される基本方程式であるが,そのままで解を求めることが困難なほど複雑である。
粘性率が一定で非圧縮性の流れに関し,流れの速度場 v ,密度ρ,圧力 p ,動粘性係数ν(=μ/ρ), 外力場(加速度)f とした時,近似方程式は,

で与えられる。
粘性流体(viscous fluid)では,粘性により,接触する物体の表面に境界層が形成され,接線方向の力(せん断応力)が作用する。
マグヌス効果(Magnus effect)
粘性を有する流体中において,回転する円柱や球が一定速度で移動する場合,又は流体が一様に流れる場合に,流に対して垂直方向の力(揚力)が働く現象をマグナス効果という。
回転する円柱や球の表面に接する流体は,粘性により引きずられ,回転速度と粘性に相応する循環 Γが発生し,移動方向や流に対して垂直方向の力 L(揚力)
L= ρU Γ
が発生する。なお,ρは流体の密度,U は一様な流の速度,Γは物体の周りの循環である。
これは,前出の循環 Γを有する翼に生ずる揚力の式(クッタ・ジュコーフスキーの定理)と一致する。
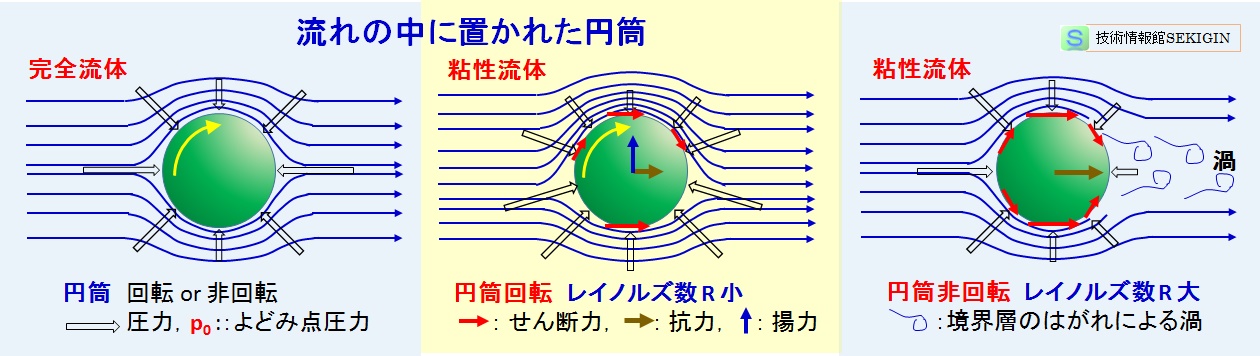
流れの中に置かれた円筒(模式図)
- ナビエストークス方程式(Navier–Stokes equations)
粘性流体の運動を記述する2階非線型偏微分方程式で,NS 方程式とも略され,運動量の流れの保存則を表す。 - 境界層(boundary layer)
1904 年にドイツの物理学者ルートヴィヒ・プラントルが発見した物体表面に沿ってできる薄い層をいう。境界層は,レイノルズ数が非常に大きいとき,粘性流体の流れにおいて,物体表面に沿って,速度勾配(渦度)がきわめて大きい薄い層である。 - 動粘性係数(kinematic viscosity)
動粘度,動粘性率ともいい,粘性率を密度で割った値で,流体の粘性の度合いを示す。 - せん断応力(shear stress)
せん断応力(剪断応力)は,接線応力やシャー応力ともいわれ,物体内部のある面に平行方向に作用する応力,すなわち面がすべるように作用する応力をいう。
ページの先頭へ
【空気抵抗(抗力)とは】
空気中を物体が移動するとき,又は空気の流れにあるとき,移動方向や空気の流れの方向と反対方向に生じる力を空気抵抗(air resistance)という。
空気抵抗は流体の抵抗として最も広く知られる用語であるが,空気に限らず気体・液体などの流体に共通する現象で,物理学では抗力(drag , fluid resistance)という。なお。流れの方向に対し垂直方向の成分を揚力(lift)ともいう。
高等学校教育では,空気抵抗は速度に比例(R=kv)と紹介しているが,これは,雨滴など小さな球体が流体中を沈降する際の終端速度を表すストークスの式(Stokes' law)を導く際の仮定で,空気抵抗の影響を理解させる目的で使用されている。
ストークスの式が成立するのは物体の寸法が小さい,流体の密度が小さく粘性が高いなどレイノルズ数が小さい場合である。従って,実際に起きる多くの現象(空気抵抗を考慮した運動)の理解には不適切である。
空気抵抗の大きさは,物体の形,大きさ,速さで変化し,一般化するのは困難といわれている。主要な空気抵抗は,物体の形状に依存する圧力抵抗(pressure drag),摩擦抵抗(friction drag)である。
圧力抵抗は慣性抵抗(inertial resistance)ともいわれ,物体表面に垂直に働く圧力の合力から成る抵抗で,概ね速度の 2 乗に比例する。圧力抵抗(慣性抵抗)は,物体の形状を流線形にすることで,圧力抵抗を著しく小さくできるが,その他の多くの形状では,圧力抵抗が主要な抵抗として作用する。
摩擦抵抗は粘性抵抗(viscous drag)ともいわれ,進行方向と平行の表面に働く空気の粘性力の合力から成る抵抗で,概ね速度に比例する。
圧力抵抗と摩擦抵抗は,物体の形状に依存するのでまとめて形状抵抗(form drag)ともいわれ,速度のほぼ 2 乗に比例する例が多い。
なお,物体の形状によっては,翼の様に揚力の発生する場合は,副次的に誘導抵抗(induced drag)が発生する。
高速船舶や音速を超える航空機では,圧力変化で発生する波による造波抵抗(wave‐making drag)が加わる。
【参考:基礎用語】
- 誘導抵抗(induced drag)
翼の揚力発生で副次的に発生する抵抗をいう。例えば,揚力の発生と同時に翼端で発生する翼端渦により気流を下げる方向の抵抗(ドラッグ成分)が働く。 - 造波抵抗(wave‐making drag)
水などの液体の上を動く物体(船舶など)が受ける抵抗の 1 つで,船の航走時に波を作るためのエネルギーに相当する抵抗で船の速度の 2 乗に比例する。
音速など高速で飛行する航空機においても,大気の圧縮(衝撃波の形成)による造波抵抗が発生する。
ページの先頭へ
【レイノルズ数とは】
レイノルズ数(Reynolds number :記号 Re )は,概念をストークスが提唱(1851年)し,イギリスの物理学者オズボーン・レイノルズ(Osborne Reynolds,1842年~ 1912年)の業績に因んで命名された。
レイノルズ数とは,流体の慣性力(inertial force)と粘性力との比で定義される。
慣性力は,質量×加速度で定義されるので,密度ρ,流速 U の流体の慣性力は,

と表される。なお,L は特性長さで,円柱の場合は半径( a )や直径( 2a )が用いられる。
単位面積当たりの接線方向の力(粘性力)がせん断応力(shear stress)なので,粘性係数(Coeffcient of viscosity),をμとすると,粘性力は,せん断応力×面積で定義され,
![]()
と表される。
従って,レイノルズ数 Re は,
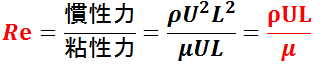
で与えられる。なお,粘性係数と密度の比 μ/ρ(=ν )は,動粘性係数(Kinematic viscosity)という。
レイノルズ数は,粘性流体の流れにおける粘性力と慣性力の比を表わすので,レイノルズ数の小さい流れは,粘性の影響による減衰効果が大で,安定した流れである。一方,レイノルズ数が大きい流れは,一般に不安定で乱流になりやすい。
一般的に,一様な流れの中に円柱を固定した場合は,Re 1 を超えると渦が発生し始め,Re 40 を超えるとカルマン渦の発生,Re 1000 以上で乱れた状態(乱流状態)になるといわれている。
層流から乱流に移行するレイノルズ数は一概に決められず,物体の形状,流路により経験的に求められる。例えば,円管内の流れでは,2300 ~ 4000 といわれ,翼形状では,104 ~106 などともいわれている。
【参考:基礎用語】
- レイノルズ(Osborne Reynolds)
オズボーン・レイノルズ(1842年~1912年)は,アイルランド生まれのイギリスの物理学者。レイノルズ数,レイノルズの輸送定理などで知られる。 - 粘性力
明確な定義はないが,一般には流体内部に速度勾配があるとき,速度を一様にするような向きの接線応力(内部摩擦)をいう。 - 慣性力(inertial force)
並進加速度系,回転座標系,及びこれらの合成系がある。この座標系ではニュートンの運動方程式は成り立たないが,見かけの力を導入することで,ニュートンの運動方程式と同形の運動方程式で記述できる。
見かけの力は,慣性系から観測した場合に見られる力(真の力)に加えて,運動方程式を満たすために導入された観測者自身の運動に依存する力である。
慣性力には反作用が加えられる物体が無いので,慣性力と真の力とは反作用の存在により区別できる。
ページの先頭へ
【流体の抗力とは】
抗力で紹介したように,日本語の抗力には,ここで扱う流体の抗力(drag)の他に,物体 A が物体 B に接触し,物体 A が物体 B 力を及ぼすときの固体物体間の相互作用としての抗力(reaction)がある。
なお,抗力(drag)は,次に紹介するように物体や流体の速度に依存する力であるが,抗力(reaction)は,速度に依存しない力であり,定義が全く異なる力である。
流体による抗力(drag)は,気体・液体中を運動する物体,又は流体中に置かれた物体に,物体の運動と逆向き,流体の流速と同じ向きに働く力である。
抗力は,レイノルズ数の解説で紹介したように,概ねで速度に比例する粘性力,概ね速度の 2 乗に比例する慣性力で構成される。
流体の密度ρ,物体と流体の相対速度 V ,投影面積など物体の代表面積 S ,抗力係数 CD としたとき抗力 D は,

で表される。
抗力係数 (drag coefficient , resistance coefficient)
一様な流れの中に置かれた物体が流体から受ける流体力のうち流れ方向の成分である抗力の無次元数と定義され,実験的に求められる値で,流れに対する物体の形状(迎え角)・レイノルズ数(流体の粘性・速さ),マッハ数によって変化する。
形状が相似な物体の場合には,抗力係数はレイノルズ数のみの関数となり,空気などの圧縮性流体中ではレイノルズ数とマッハ数の関数になる。なお,マッハ数は,流体の相対速度と音速の比で,流れ場における圧縮性の影響の程度を表し,空気中では,マッハ数 0.3 より大きい場合に圧縮性の影響が無視できなくなる。
一般的には,抗力は,レイノルズ数が小さい場合は概ね速度に比例し,レイノルズ数が大きい場合は概ねで速度の 2 乗に比例する。また,物体の相似比の 2 乗,すなわち投影面積に比例する。
ページの先頭へ
【ストークスの式について】
ストークスの式(Stokes' law)とは,流体中を沈降する微粒子の終端速度(terminal velocity)を表す式で,沈降法による粒子径測定などに用いられている。
一旦終端速度に達すると等速度運動になる。
終端速度に達するまでの時間を緩和時間といい,粒子径が小さい物体の緩和時間は短く,大きい粒子ではより長い緩和時間を要する。
終端速度 Vs ,粒子の直径 Dp ,粒子の密度ρp ,流体の密度ρf ,流体の粘性係数(粘度)μ ,重力加速度 g とした時,ストークスの式は,

で与えられる。
ストークスの式は,球形の小さい粒子で,レイノルズ数 Re 2 より小さい条件で,成立する。粒子の形状が不定形の場合や大きい場合には,流体から受ける抗力が計算値からずれるため適用しない方がよい。
ストークスの式の内容
粒子の落下速度に依存しない力
粒子の密度ρp ,流体の密度ρf としたとき,流体中を落下する半径 r の球体に働く浮力 Fb と重力 Fg は,
![]()
粒子の落下速度に依存する抗力
前出したように,抗力 D は,流体の密度ρ,物体と流体の相対速度 V ,投影面積など物体の代表面積 S(=πr2 ),抗力係数 CD とすると
![]()
で表される。
ここで,球形の物体の場合,抗力係数 CD は,一般的には,レイノルズ数 Re の大きさで Re< 2( CD = 24/ Re ),2 <Re< 500( CD = 10/ Re1/2 ),500 <Re< 105 ( CD = 0.44 )で与えられる。
レイノルズ数 Re は,前出したように,
![]()
で与えられる。なお,μは流体の粘性係数,ρは流体の密度(ここではρf を用いる), U は流速(ここでは相対速度 V を用いる),L は特性長さ(球の場合は直径( 2r )が用いられる)である。
従って,レイノルズ数 Re < 2 の条件で,抗力 D は,
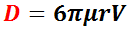
となる。
終端速度 Vs では,下向きと上向きの力が釣り合う重力=抗力+浮力の関係が得られるので,レイノルズ数 Re < 2 の条件では,


となり,前出のストークスの式が得られる。
【参考:基礎用語】
- 終端速度(terminal velocity)
重力場において,浮力や抗力などの粒子に作用する上向きの力と下向きの重力とが釣り合ったときの速度である。浮力は粒子の速度に依存しないが,前述のように,抗力は粒子と流体の相対速度に依存するため,落下速度の増加と共に抗力が増加する。 - 空気抵抗(air resistance)
半径 r の完全な球に作用する空気抵抗 Fd について,一般的には次式が多く利用されている。
Fd = 6πμr V + 1/2 Cdρπ r2V2
なお,粘性率μ,密度ρは温度,湿度,気圧の影響を受けるので,空気抵抗の計算ではこれらを考慮した補正が必要である。 - 緩和時間(relaxation time)
系が非平衡から平衡に向かって変化するなど,条件の変化が起きた時,新しい状態に移行するまでの時間をいう。
ページの先頭へ